Calculateur de Volume
Calculer une pièce en m³, ou volume en mètre cube, est une tâche courante dans de nombreuses situations, que ce soit pour planifier l’aménagement d’une pièce, déterminer les besoins en chauffage ou encore calculer les coûts de travaux.
À ce propos, il est souvent utile d’utiliser un simulateur en ligne pour obtenir un résultat précis de votre calcul en m³. C’est pourquoi, nous vous proposons ci-dessus une calculatrice en ligne servant à calculer rapidement de calculer un m3 d’une pièce.
D’autre part, nous profitons de ce thème pour vous expliquer quelques informations à ce sujet. Ainsi, vous trouverez ci-dessous une explication détaillée de ce qui se cache derrière ce calcul.
Le mètre cube : qu’est-ce que c’est ?
En premier lieu, il est important de comprendre cette unité de mesure.
Le mètre cube (noté m³) est une unité de mesure de volume dans le système international d’unités. Comme son nom l’indique, un mètre cube représente le volume d’un cube dont chaque côté mesure un mètre. Imaginez un cube parfait où la longueur, la largeur et la hauteur sont toutes égales à un mètre.
Cette unité est normalisée selon la norme ISO 31-1. Cela signifie que partout dans le monde, un mètre cube a la même taille et le même volume. Cette standardisation est cruciale car elle permet aux gens de différents pays ou industries de communiquer et de travailler ensemble avec des mesures précises et cohérentes.
Comment calculer un m3 ?
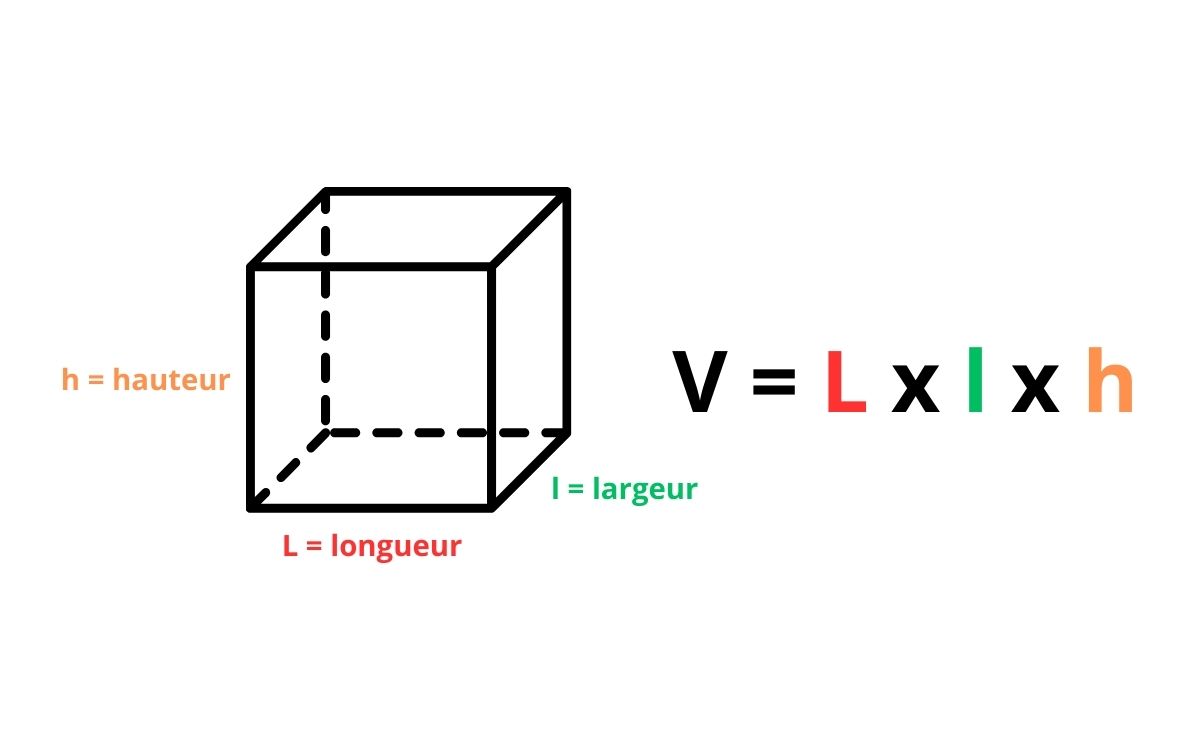
Il existe une formule générale permettant de calculer le volume d’un objet : V = L × l × h, où V représente le volume, L la longueur, l la largeur et h la hauteur. Cette formule s’applique à tous les objets de forme rectangulaire ou carrée. Bien sûr, il est nécessaire d’avoir ces trois dimensions pour pouvoir réaliser le calcul.
Prenons un exemple concret : si vous souhaitez connaître le volume en m3 d’un carton ayant une longueur de 2 mètres, une largeur de 1,5 mètre et une hauteur de 0,8 mètre, il suffit d’appliquer la formule :
- V = 2 m × 1,5 m × 0,8 m
- Soit V = 2,4 m³.
Neutralement, la même formule peut être utilisée avec des unités de mesure différentes du mètre (comme le centimètre ou le millimètre), à condition de convertir ensuite les valeurs obtenues en mètre cube. Pour ce faire, il suffit de respecter les équivalences suivantes :
- 1 mètre = 100 centimètres = 1.000 millimètres
Calculer le volume d’un cylindre
La technique pour déterminer les m3 d’un objet cylindrique diffère légèrement puisqu’il faut prendre en compte la forme spécifique de l’objet : V = π × R² × h, où V est le volume, π (pi) représente environ 3,14159, R est le rayon et h la hauteur. En pratique, avec un cylindre mesurant 1 mètre de diamètre et 2 mètres de haut :
- R = 0,5 m (le rayon est égal à la moitié du diamètre)
- V = 3,14159 × (0,5)² × 2 = 1,5708 m³
Déterminer les m3 d’un cône
Pour réaliser ce type de calcul, il convient d’utiliser la formule suivante : V = (1/3) × π × R² × h, avec V pour le volume, π (pi) valant environ 3,14159, R représentant le rayon et h la hauteur. Si notre cône mesure 1 mètre de diamètre et 3 mètres de haut :
- R = 0,5 m
- V = (1/3) × 3,14159 × (0,5)² × 3 = 0,7854 m³
Convertir des litres en m3
Dans certains cas, il est possible de calculer directement le volume en m3 d’un objet, notamment lorsque les dimensions sont déjà exprimées dans cette unité. C’est typiquement le cas pour des réservoirs ou des bacs indiquant leur capacité en litres : il suffit de diviser ce chiffre par 1.000 pour obtenir la valeur en mètres cubes.
Ainsi, un bac de 4.500 litres aura un volume de :
- 4.500 / 1.000 = 4,5 m³
De même, une piscine ayant une contenance de 50 m³ représentera :
- 50.000 litres d’eau !
En suivant ces conseils, vous devriez être capable de maîtriser le calcul du volume en m3 pour la majorité des pièces que vous rencontrerez dans votre quotidien.